(Adjusted) survival curves

Randomized trials and observational studies frequently present survival curves to show time-to-event outcomes, and allow comparisons between two or more groups.

Note

In this chapter, you will learn how to:

  1. Plot Kaplan-Meier curves
  2. Plot adjusted (‘confounding-corrected’) survival curves, and the difference between two survival curves over time, using flexible parametric survival models
  3. Plot time-varying hazard ratios, which can be useful when the proportional hazards is violated
Critical assumptions
  1. Censoring
  2. Competing risks
  3. Immortal time bias
  4. Clustering

In this chapter, we’ll use data from 2982 patients with primary breast cancer who were included in the Rotterdam tumor bank. Our primary comparison is between patients who did and did not receive hormonal treatment

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.4     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
Loading required package: Hmisc

Attaching package: 'Hmisc'

The following objects are masked from 'package:dplyr':

    src, summarize

The following objects are masked from 'package:base':

    format.pval, units
Loading required package: ggpubr

Attaching package: 'survminer'

The following object is masked from 'package:survival':

    myeloma
library(flexsurv)

os_dat <- survival::rotterdam
knitr::kable(head(rotterdam))
pid year age meno size grade nodes pgr er hormon chemo rtime recur dtime death
1393 1 1992 74 1 <=20 3 0 35 291 0 0 1799 0 1799 0
1416 2 1984 79 1 20-50 3 0 36 611 0 0 2828 0 2828 0
2962 3 1983 44 0 <=20 2 0 138 0 0 0 6012 0 6012 0
1455 4 1985 70 1 20-50 3 0 0 12 0 0 2624 0 2624 0
977 5 1983 75 1 <=20 3 0 260 409 0 0 4915 0 4915 0
617 6 1983 52 0 <=20 3 0 139 303 0 0 5888 0 5888 0

First, we’ll plot Kaplan-Meier curve to show the unadjusted association between hormonal therapy and overall survival.

theme_boers <- function(){
theme(text=element_text(family="Corbel", colour="black"), 
      plot.margin = margin(0.2,1,0,0,"cm"), #prevent x axis labels from being cut off
      plot.title = element_text(size=20),
      panel.grid.major = element_blank(), 
      panel.grid.minor = element_blank(),
      axis.text.x=element_text(size=20, colour="black"), 
      axis.text.y=element_text(size=20, colour="black"), 
      axis.title.x = element_text(size=20), 
      axis.title.y = element_text(size=20), 
      axis.line = element_line(colour = 'black', linewidth = 0.25),
      axis.ticks = element_line(colour = "black", linewidth = 0.25),
      axis.ticks.length = unit(4, "pt"),
      axis.minor.ticks.length = unit(2, "pt"))
}

os_summary <- surv_summary(survfit(Surv(dtime, death)~hormon, 
                                   data=os_dat), data=os_dat)
os_summary <- as.data.frame(os_summary)

os_temp <- os_summary[1,]
os_temp[2,] <- os_temp[1,]

os_temp$time <- 0
os_temp$n.risk <- c(2643, 339)
os_temp$strata <- c("hormon=0", "hormon=1")
os_temp$hormon <- c(0,1)

os_summary <- rbind(os_temp, os_summary)

os_summary$time <- os_summary$time/365.24

os_summary_0 <- subset(os_summary, hormon==0 & time<=10)
os_summary_1 <- subset(os_summary, hormon==1 & time<=10)
bg_line_dat <- data.frame("x"=rep(0,6), "xend"=rep(10.5,6), 
                   "y"=seq(0,1,by=0.2), "yend"=seq(0,1,by=0.2))

gg <- ggplot(data=os_summary_0, aes(time,surv)) + 
  theme_minimal() + theme_boers() + 
  geom_segment(data=bg_line_dat, aes(x=x, xend=xend, 
                   y=y, yend=yend),
               col="#e3e4e5") +
  geom_step(colour="#374e55", 
            linewidth=1) + 
  geom_ribbon(aes(ymin=lower, ymax=upper), fill="#374e5530") +
  geom_step(data=os_summary_1, aes(time,surv), 
            colour="#df8f44", linewidth=1) +
  geom_ribbon(data=os_summary_1, 
              aes(ymin=lower, ymax=upper), fill="#df8f4430") +
  #geom_smooth(method="gam", formula = y ~ s(x, bs = "cs")) +
  annotate("text", x=6, y=0.815, label="No hormonal therapy", 
           fontface=2, colour="#374e55") +
  annotate("text", x=3, y=0.615, label="Hormonal therapy", 
           fontface=2, colour="#df8f44") +
  scale_x_continuous(breaks=seq(0,10,by=1),
                     labels=seq(0,10,by=1),
                     minor_breaks = seq(0,10,by=0.5),
                     expand = c(0,0)) +
    scale_y_continuous(breaks=seq(0,1,by=0.2),
                     labels=c(0,0.2,0.4,0.6,0.8,"1.0"),
                     minor_breaks = seq(0,1,by=0.1),
                     expand = c(0,0)) +
  guides(x = guide_axis(minor.ticks = TRUE),
    y = guide_axis(minor.ticks = TRUE)) +
  coord_cartesian(xlim=c(0,10.5), ylim=c(0,1), clip = "off") +
  xlab("Time after diagnosis (years)") + ylab("Survival probability")

gg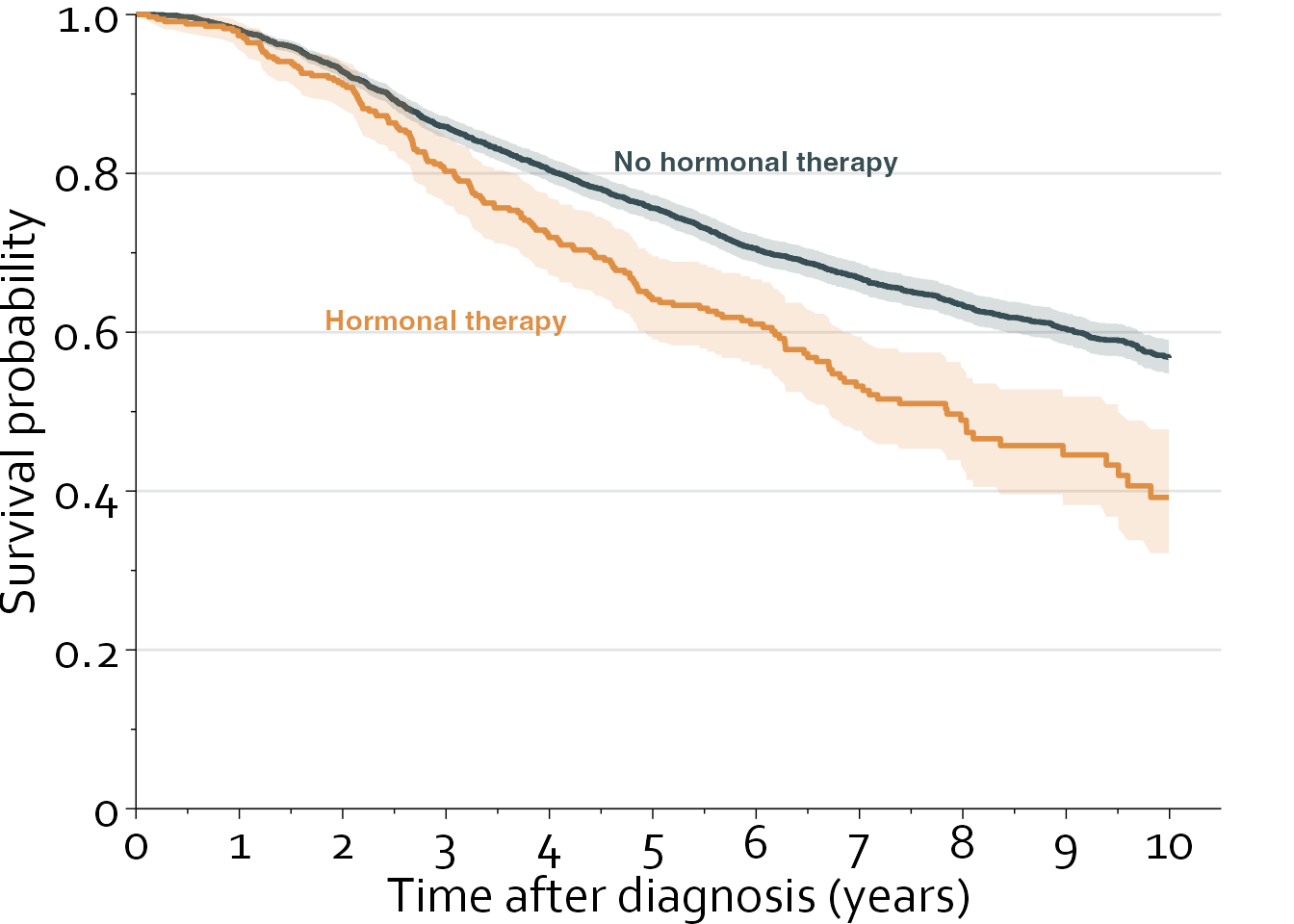

We’ll use Cox regression to estimate the unadjusted hazard ratio:

cph(Surv(dtime, death) ~ hormon, 
               data=os_dat)
Cox Proportional Hazards Model

cph(formula = Surv(dtime, death) ~ hormon, data = os_dat)

                       Model Tests     Discrimination    
                                              Indexes    
Obs      2982    LR chi2     21.12     R2       0.007    
Events   1272    d.f.            1    R2(1,2982)0.007    
Center 0.0471    Pr(> chi2) 0.0000    R2(1,1272)0.016    
                 Score chi2  23.69     Dxy      0.042    
                 Pr(> chi2) 0.0000                       

       Coef   S.E.   Wald Z Pr(>|Z|)
hormon 0.4144 0.0853 4.86   <0.0001 
exp(0.4144 + c(-1.96,0,1.96)*0.0853)
[1] 1.280451 1.513462 1.788877

The unadjusted (‘crude’) hazard ratio is 1.51 (95% confidence interval, 1.28 to 1.79; P<0.0001), indicating that hormonal therapy is associated with shorter overall survival. We’ll now adjust for several potential confounders, including age, menopausal state, and tumor size:

cph_os <- cph(Surv(dtime, death) ~ hormon + rcs(age, 4) + meno + 
                 size + grade + rcs(log(nodes+1),4) + 
                 rcs(log(pgr+1),4) + rcs(log(er+1), 4), 
               data=os_dat)

dd <- datadist(os_dat)
options(datadist = "dd")

summary(cph_os)
             Effects              Response : Surv(dtime, death) 

 Factor            Low High   Diff.  Effect    S.E.     Lower 0.95 Upper 0.95
 hormon             0    1.00   1.00 -0.269790 0.090741 -0.44764   -0.09194  
  Hazard Ratio      0    1.00   1.00  0.763540       NA  0.63914    0.91216  
 age               45   65.00  20.00 -0.145610 0.142480 -0.42487    0.13364  
  Hazard Ratio     45   65.00  20.00  0.864490       NA  0.65386    1.14300  
 meno               0    1.00   1.00  0.372610 0.127110  0.12347    0.62175  
  Hazard Ratio      0    1.00   1.00  1.451500       NA  1.13140    1.86220  
 grade              2    3.00   1.00  0.276760 0.071245  0.13713    0.41640  
  Hazard Ratio      2    3.00   1.00  1.318900       NA  1.14700    1.51650  
 nodes              0    4.00   4.00  0.973510 0.074782  0.82694    1.12010  
  Hazard Ratio      0    4.00   4.00  2.647200       NA  2.28630    3.06510  
 pgr                4  198.00 194.00 -0.376860 0.099832 -0.57252   -0.18119  
  Hazard Ratio      4  198.00 194.00  0.686020       NA  0.56410    0.83428  
 er                11  202.75 191.75  0.010873 0.091326 -0.16812    0.18987  
  Hazard Ratio     11  202.75 191.75  1.010900       NA  0.84525    1.20910  
 size - 20-50:<=20  1    2.00     NA  0.296260 0.066396  0.16613    0.42639  
  Hazard Ratio      1    2.00     NA  1.344800       NA  1.18070    1.53170  
 size - >50:<=20    1    3.00     NA  0.531100 0.093384  0.34807    0.71413  
  Hazard Ratio      1    3.00     NA  1.700800       NA  1.41630    2.04240

The adjusted hazard ratio for hormonal therapy is 0.76 (95% CI, 0.64 to 0.91), indicating that hormonal therapy is associated with longer overall survival.